If y=0 , then x 33x 2 =x 2 (x3)=0 so that x=0 and x=3 are the xintercepts There are no vertical or horizontal asymptotes since f is a polynomial See the adjoining detailed graph of fIf the CDF F is strictly increasing and continuous then (), ,, is the unique real number such that () = In such a case, this defines the inverse distribution function or quantile function Some distributions do not have a unique inverse (for example in the case where f X ( x ) = 0 {\displaystyle f_{X}(x)=0} for all a < x < b {\displaystyleMathematics Stack Exchange is a question and answer site for people studying math at any level and professionals in related fields It only takes a minute to sign up
Solved 1 The Graph Of F X Is Continuous And Decreasing With An X Intercept At X 0 Which Of The Following Statements Is True Course Hero
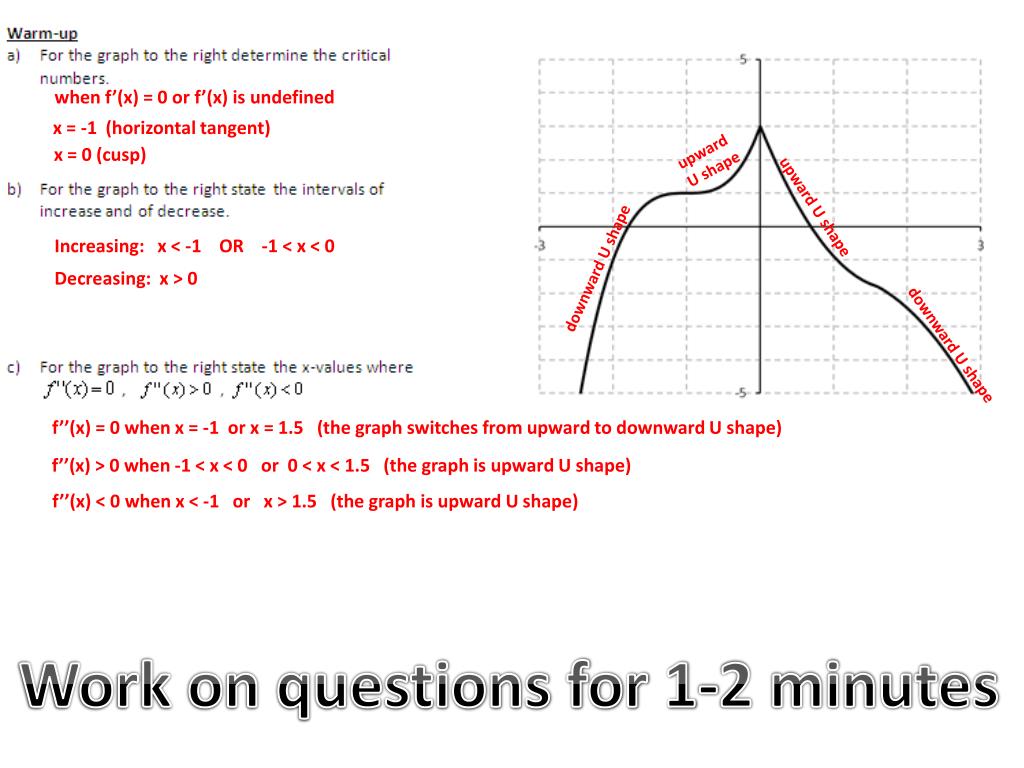
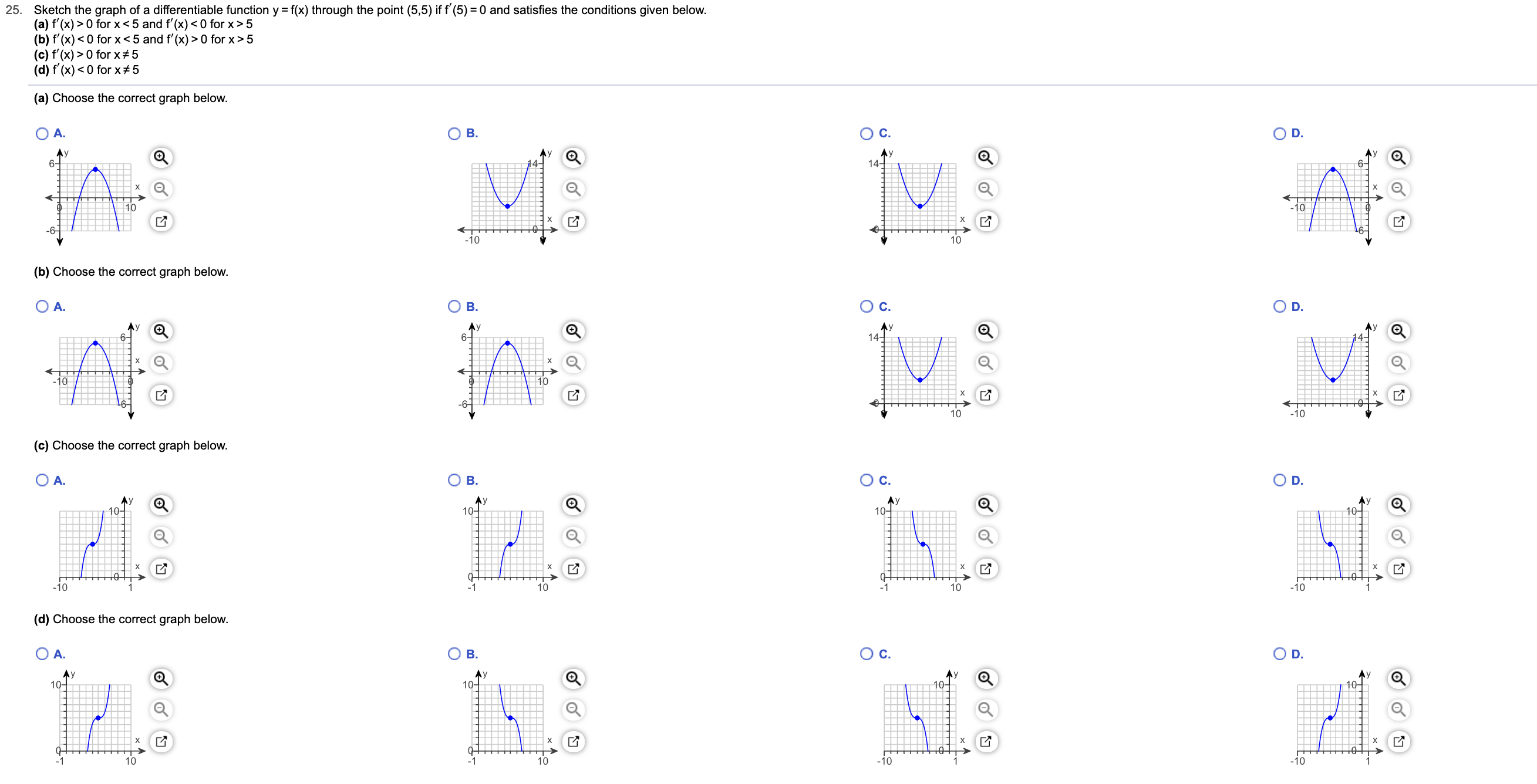
Where is f'(x) 0
Where is f'(x) 0-Graph {eq}f(x) = 3^x 1 {/eq} Graph The graph of an exponential function shows how rapidly the function increases as its input value increases Even for small changes in the input, the functionJan 28, · Example 22 The function f is defined by 𝑓 (𝑥)= { (1−&𝑥, 𝑥0)┤ Draw the graph of f (x) For x < 0 , f (x) = 1 – x We find the points to be plotted when x < 0 For x = 0 , f (x) = 1 Hence, point to be plotted is (0,1) For x > 0 , f (x) = x 1 We find the points to be plotted when x > 0 Hence we make a




Ap Calculus Ab Practice Exam Multiple Choice Problem 27 Youtube
First 100 trials done by program just incase you wanted to see the results gives x then f(x) then whether or not f(x) was prime Furthermore ignore first two tests my algorithm works but not forIff on an interval a b which means f x 0 for all x in a b then the graph of f Iff on an interval a b which means f x 0 for all x in School Georgia Institute Of Technology;F(x)dx is the area of the region under the graph of f and above the interval a,b In fact, for most functions the definite integral defines the area under the graph Before we consider some examples, let's give an obvious property of definite integrals but one worth noting Property 1 R a a f(x)dx = 0 That is, if all of the ∆x
Apr 11, 19 · (1, 1), (0, 0) Stepbystep explanation Assuming your function is the negative cube root of negative x, the two points listed above are on the curve (The negatives cancel, so the function reduces to f(x) = ∛x) The various points relative to the curve are shown in the attachmentCourse Title MAT 113;X is not equal to 0 or 1 Please explain how to get all values of x when f (x) > 0 and f (x
(a) Sketch the graph of y = f(x), given the following • f(−1) = 2;How to tell where f(x) greater than 0 or f(x) less than 0 How to tell where f(x) greater than 0 or f(x) less than 0The graph of y = f (x) is the graph of y = f (x) reflected about the yaxis Here is a picture of the graph of g(x) =(05x)31 It is obtained from the graph of f(x) = 05x31 by reflecting it in the yaxis Summary of Transformations To graph Draw the graph of f and Changes in the equation of y = f(x) Vertical Shifts y = f (x) c




The Graph Of The Function F X X Sin 21x 0 Sx S1 Is Shown Below Define F X F X Fn 1 X F F X For N 21 1 Y X Y F X
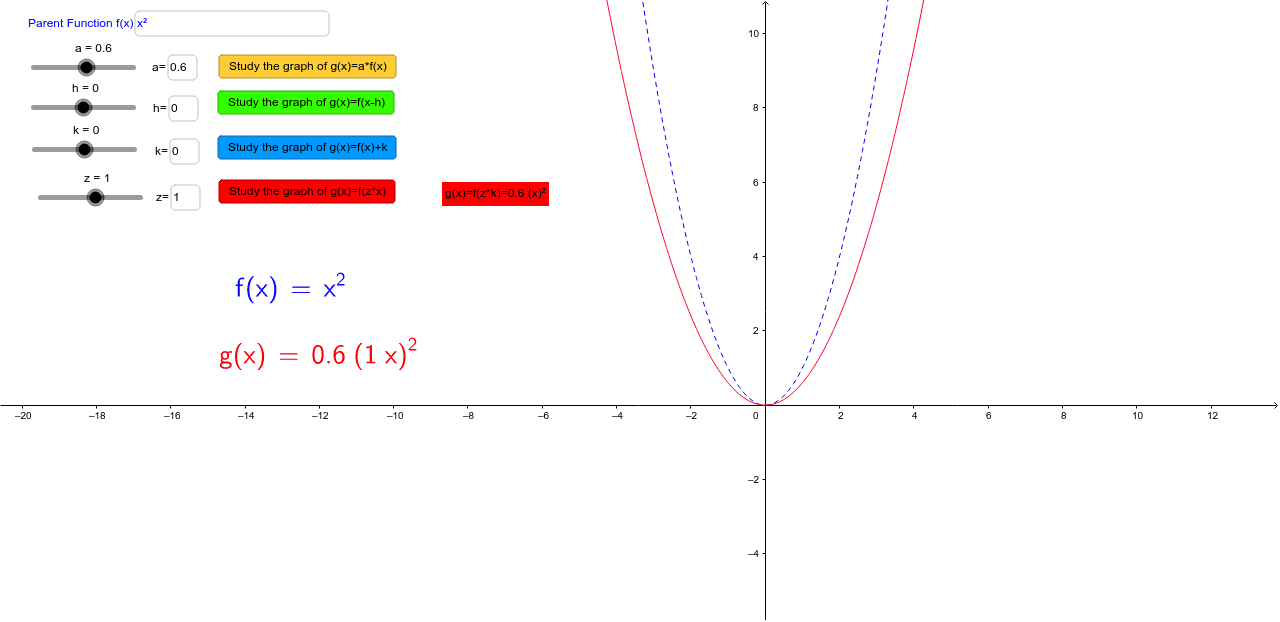



Graph Transformations Discovering Manipulating Functions Geogebra
Let us start with a function, in this case it is f(x) = x 2, but it could be anything f(x) = x 2 Here are some simple things we can do to move or scale it on the graph We can move it up or down by adding a constant to the yvalue g(x) = x 2 C Note to move the line down, we use a negative value for C C > 0 moves it up;See the answer Find all values of x such that f (x) > 0 and all x such that f (x) < 0 and sketch the graph of f 1) Answer f (x) > 0 if x < 2 or 0< x< 4 ;Here for x > 0, the graph represents a line where y = x Similarly for x < 0, the graph is a line where y = x Here both the graph lines hold true the definition of modulus functions The graph defines the domain and range of modulus function, ie the domain = R (or Real Numbers)
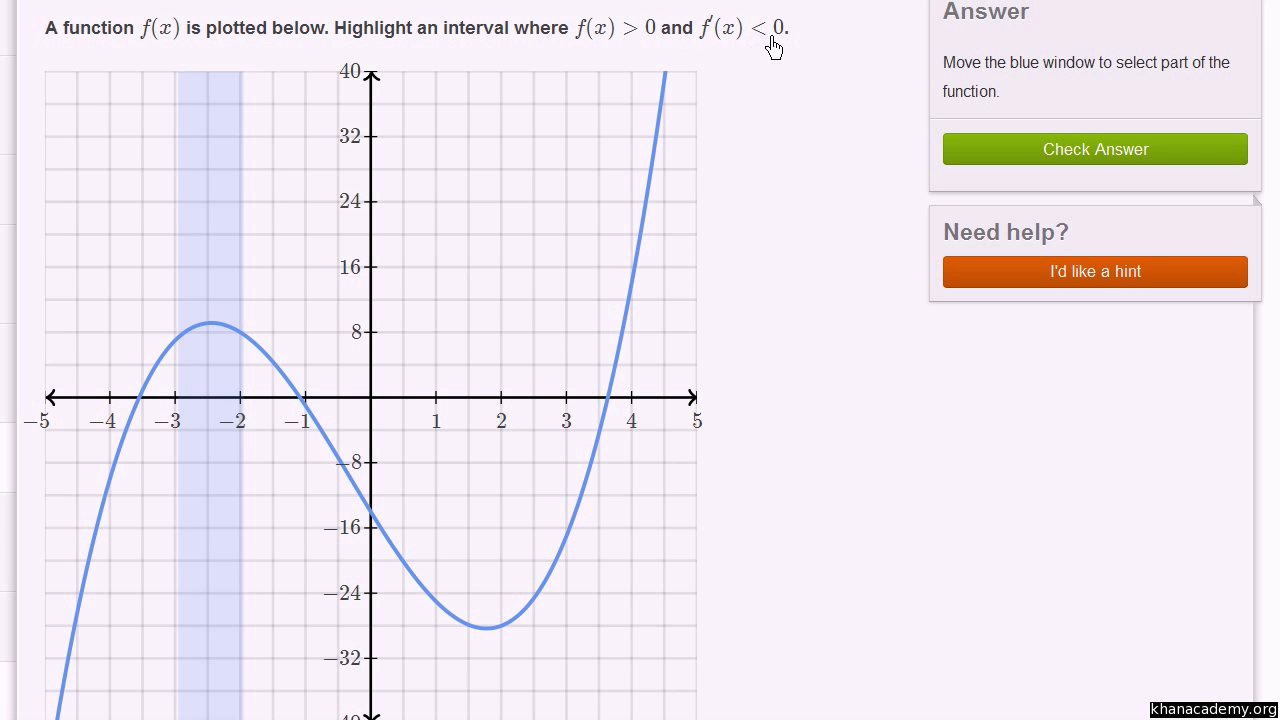



Derivative The Direction Of A Function Video Khan Academy
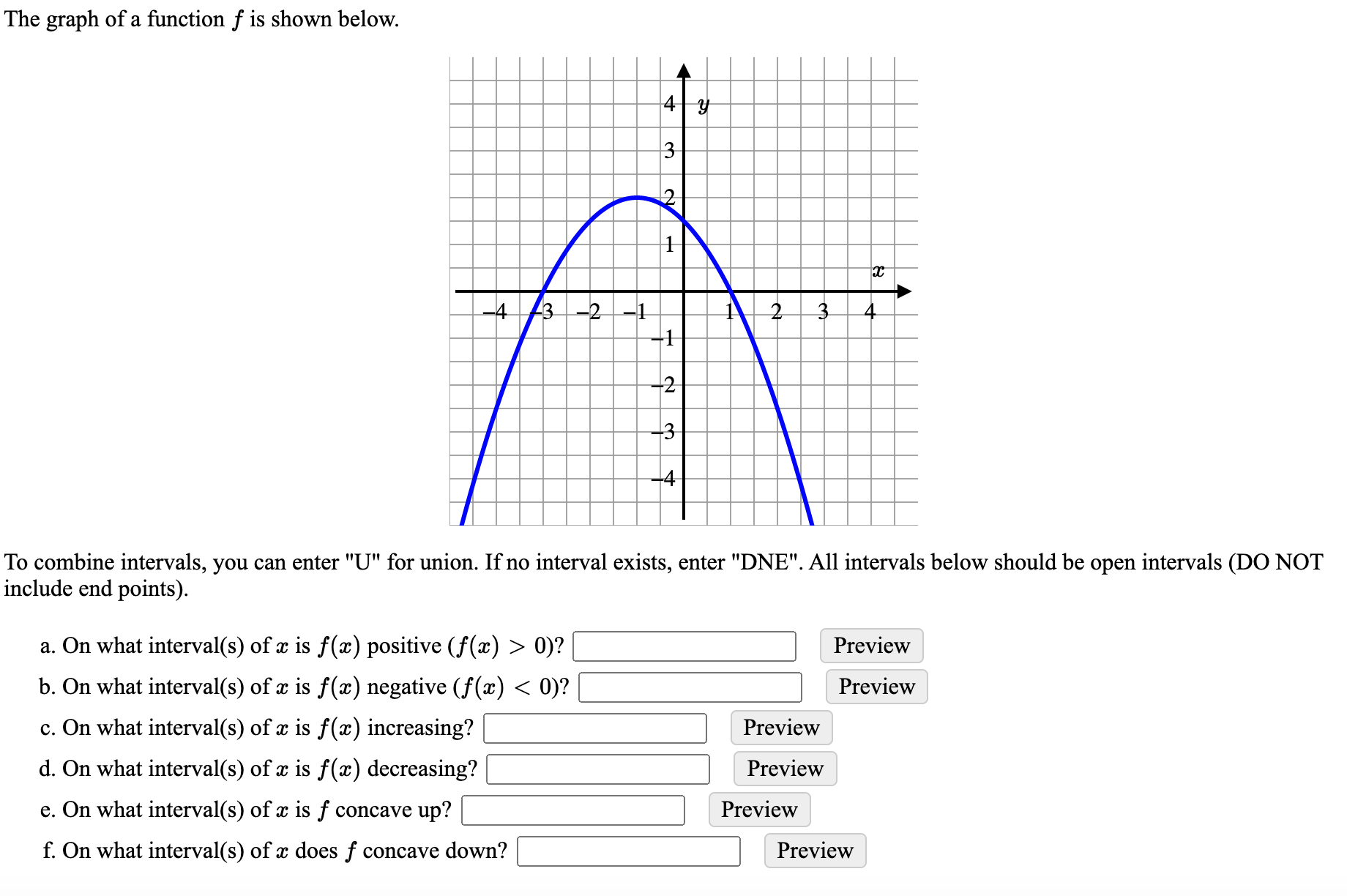



Answered The Graph Of A Function F Is Shown Bartleby
The quadratic equation g(x) = ( 3x^2 4x 5) can be written as ;F (x) < 0 if 2 < x< 0 or x > 4 2) Answer f (x) > 0 if x > 2 f (x) < 0 if x < 2 ;This is an absolute value function It forms a v shaped graph For positive xvalues, and zero, it is a line with a yintercept of zero and a slope of one y = x if x > 0 or x = 0 For negative xvalues it is a line with a yinte




Help Needed With Calculus Question Wyzant Ask An Expert



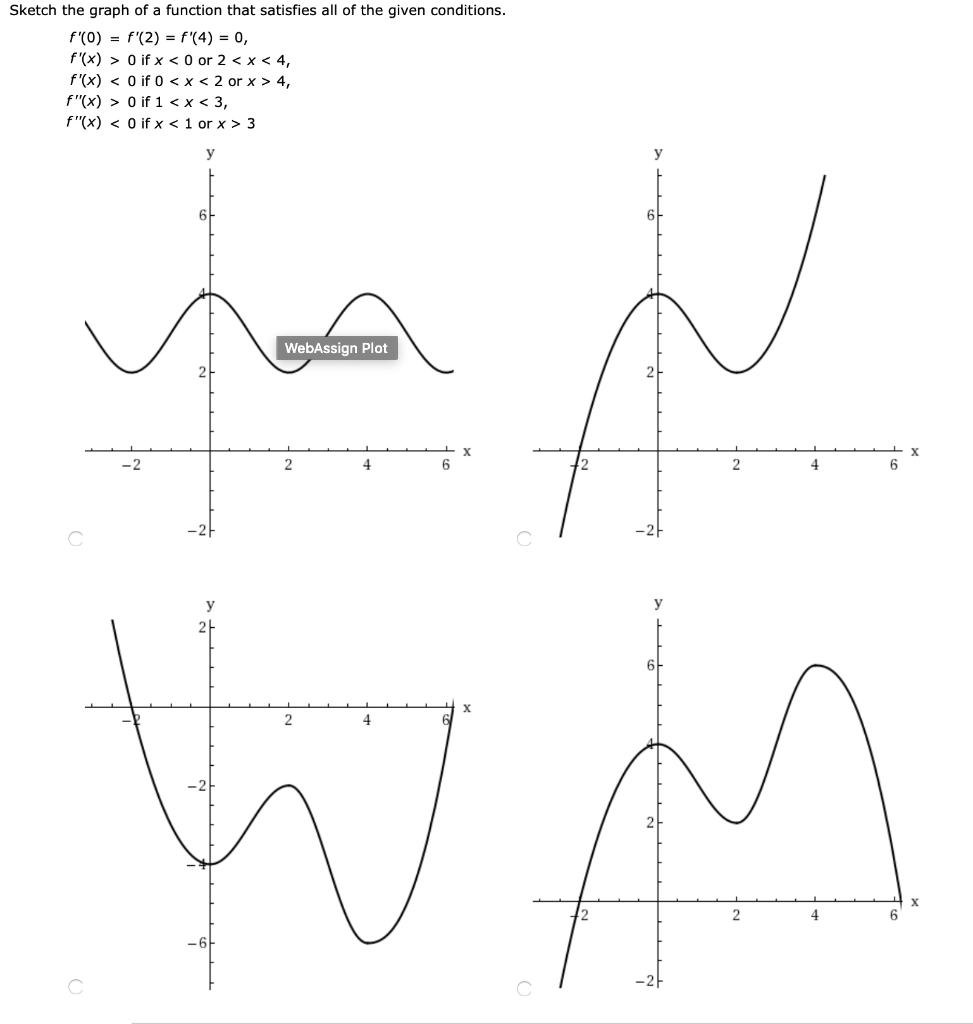
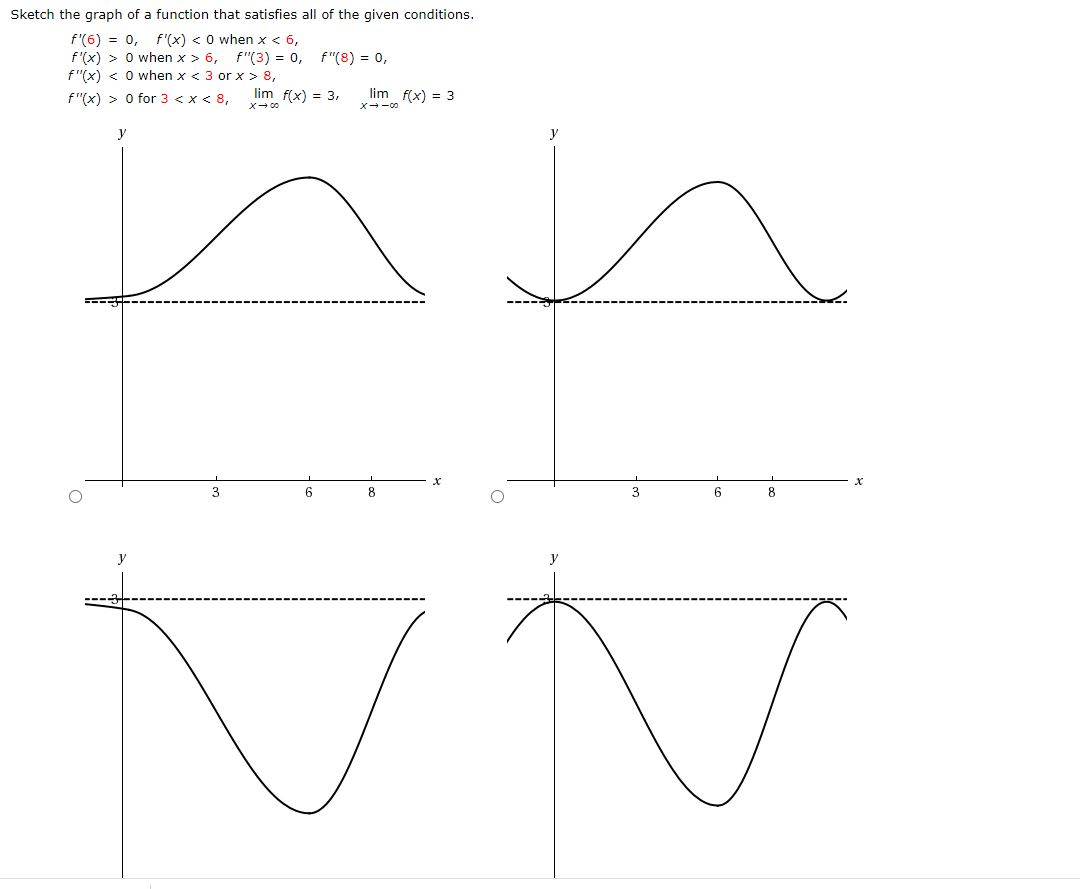
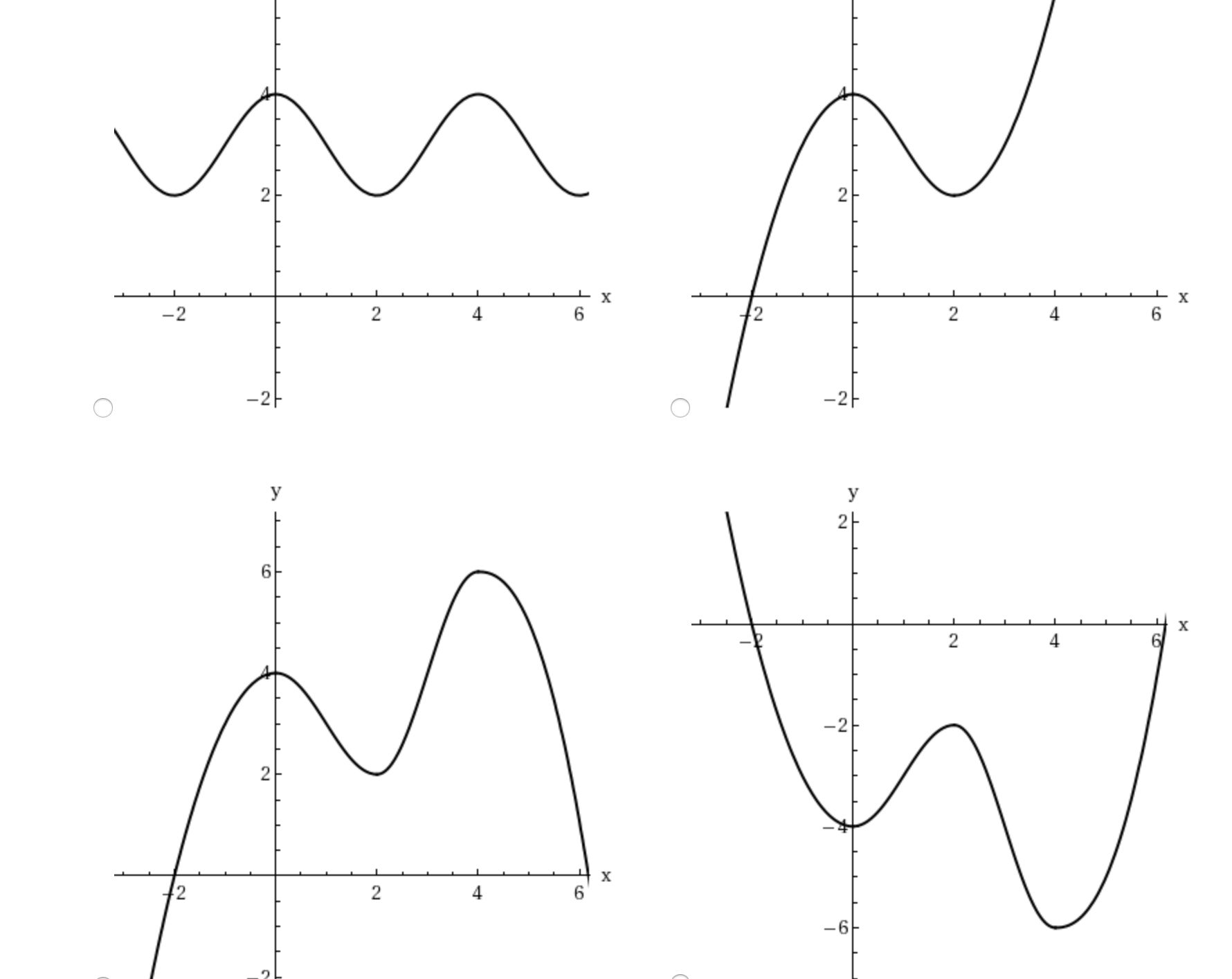
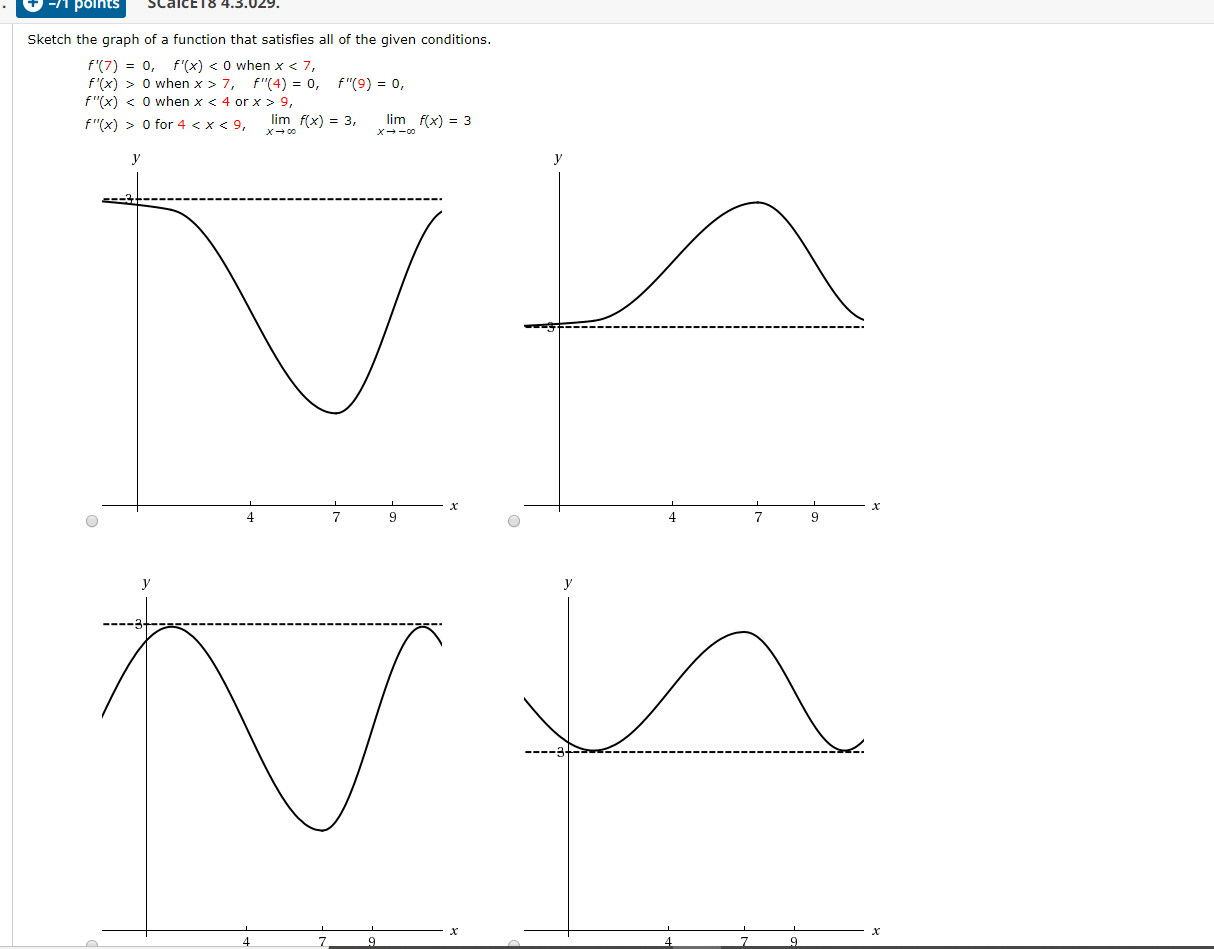
Solved 5 Details Scalcet8 4 Sketch The Graph Of A Function That Satisfies All Of The Given Conditions F X Gt 0 For All X 1 Vertical Asymp Course Hero
Oct 14, 16 · Notice that the graph of f crosses the x axis at − 3, − 2, 0, 2 and 3 Using the fact f ( x) > 0 on the interval where the graph is above the x axis, and f ( x) < 0 on the interval where the graph is below the x axis we have Find where it crosses 0 Use open intervals inSketch a possible graph for a function f(x) that has ALL the stated conditions Label your graph 7 points f(0) = 0, lim f(x) = , lim f (x) co, lim f(x) = 0, lim f(x) = 1, lim f(x) = 1 5 Given the graph of the function f 10 points 6 1210 5 6 442 1 2 4 6 8 10 12 Proctored Exam 1 docxFor example, f(x) = x 3 4x 2 4x has a relative minimum of 0 It attains this relative minimum at x = 2, so (2,0) is a turning point of the graph of f We will call the point (2,0) a relative minimum point In general, a relative extreme point is a point on the graph of f whose second coordinate is a relative extreme value of f Example 4



Solved Sketch The Graph Of Function F That Satisfies The Following Conditions Course Hero
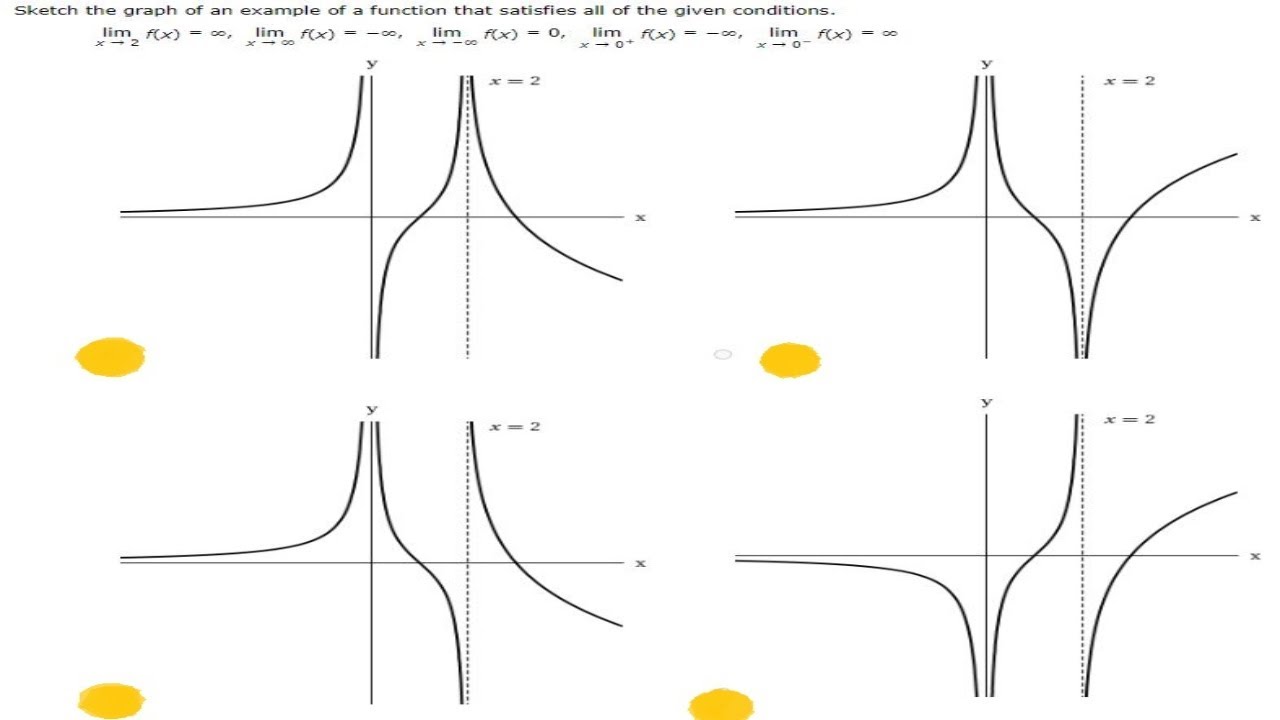



Sketch The Graph Of An Example Of A Function That Satisfies The Given Conditions Limx 2f X Youtube
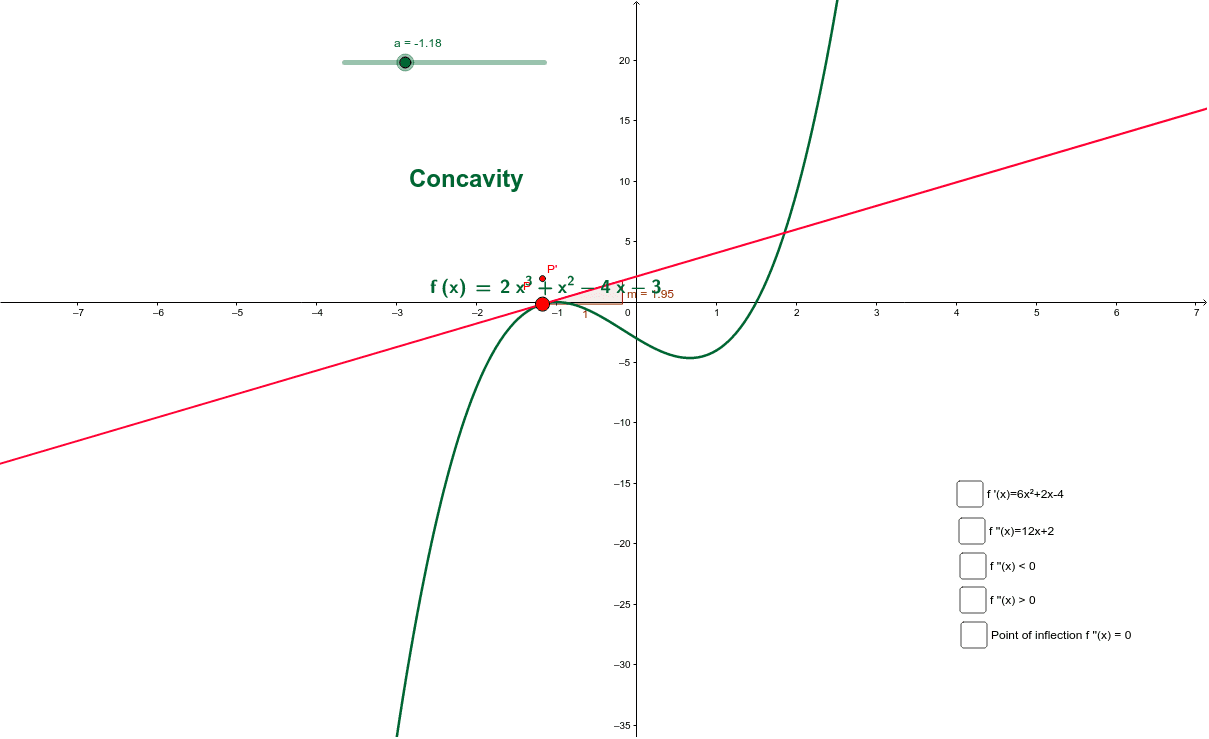
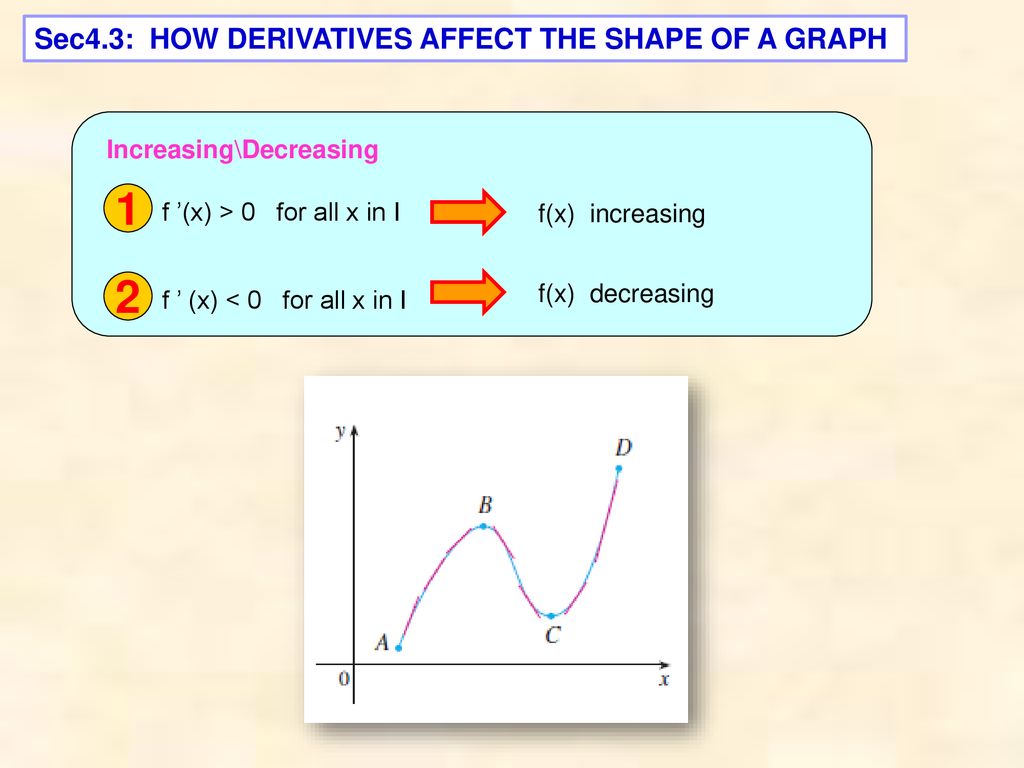
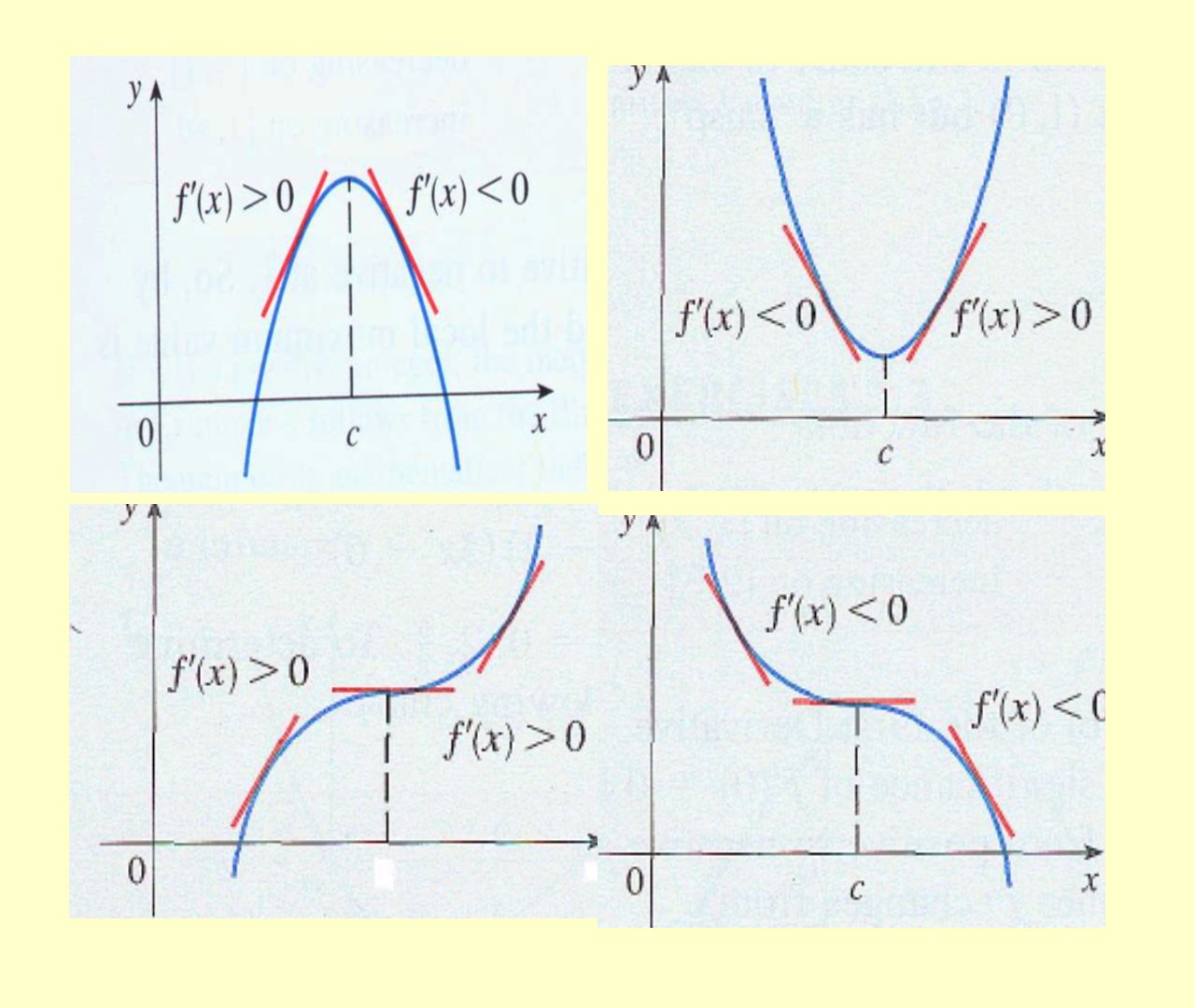
Increasing/Decreasing Test If f′(x) > 0 for all x ∈(a,b), then f is increasing on (a,b) If f′(x) < 0 for all x ∈(a,b), then f is decreasing on (a,b) First derivative test Suppose c is a critical number of a continuous function f, then Defn f is concave down if the graph of fApr 10, 19 · The graph of f ′(x), the derivative of x, is continuous for all x and consists of five line segments as shown below Given f (0) = 6, find the absolute maximum value of f (x) over the interval 0, 3 a) 0 b) 8 c) 10 d) 16Lim x→∞ f(x) = 0;



Multiplicative Inverse Wikipedia




Answered How Derivatives Section 4 3 8 The Bartleby
This preview shows page 187 191 out of 4 pages Solution First we draw the graph of f for x ∈ 0, 2 according to the given definition Then we use the fact that f is an odd function and that its graph must be symmetric with the respect to the origin (c) Draw the graph of the function g (x) =2 f (x1) 1 Solution 4 6 (a) Let f (x) = x 1 x and g (x) = x 1 x1The graph of a function $\,f\,$ is shown at right The solution set of the inequality '$\,f(x)\gt 0\,$' is shown in purple It is the set of all values of $\,x\,$ for which $\,f(x)\,$ is positiveThe problem is that the function is not defined when x y = 0, and to have a limit you must be able to evaluate f (x, y) for all (x, y) sufficiently close to 0 If they specify f ( x , − x ) = 0
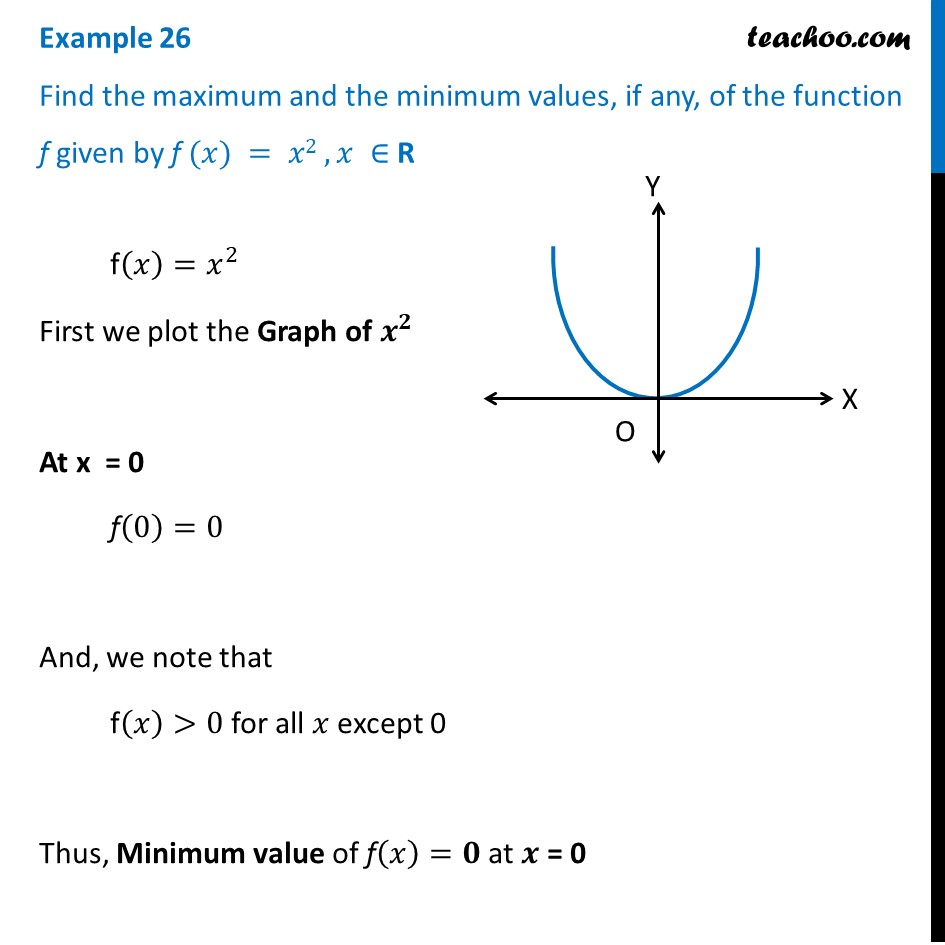



Example 26 Find Maximum And Minimum Values Of F X X2




Extreme Values Definitions
Uploaded By chestypullersarms Pages 19 This preview shows page 19 out of 19 pagesSince we're looking for f(x)=0, we're looking for y=0 since y and f(x) can be interchanged In other words, we are looking for the xintercept, since y=0 for all xintercepts So we substitute 0 in for f(x) and we get Now we solve for x Add 12 to both sides Divide both sides by 3 This will isolate xJan 02, 17 · HSBC244 has shown a nice graph that has derivative #f'(3)=0# Here are couple of graphs of functions that satisfy the requirements, but are not differentiable at #3# #f(x) = abs(x3)5# is shown below graph{y = abs(x3)5 14, 25, 616, 1185} #f(x) = (x3)^(2/3) 5# is shown on the next graph




The Graph Of The Function F X Is Shown Below When F X 0 Determine X Brainly Com
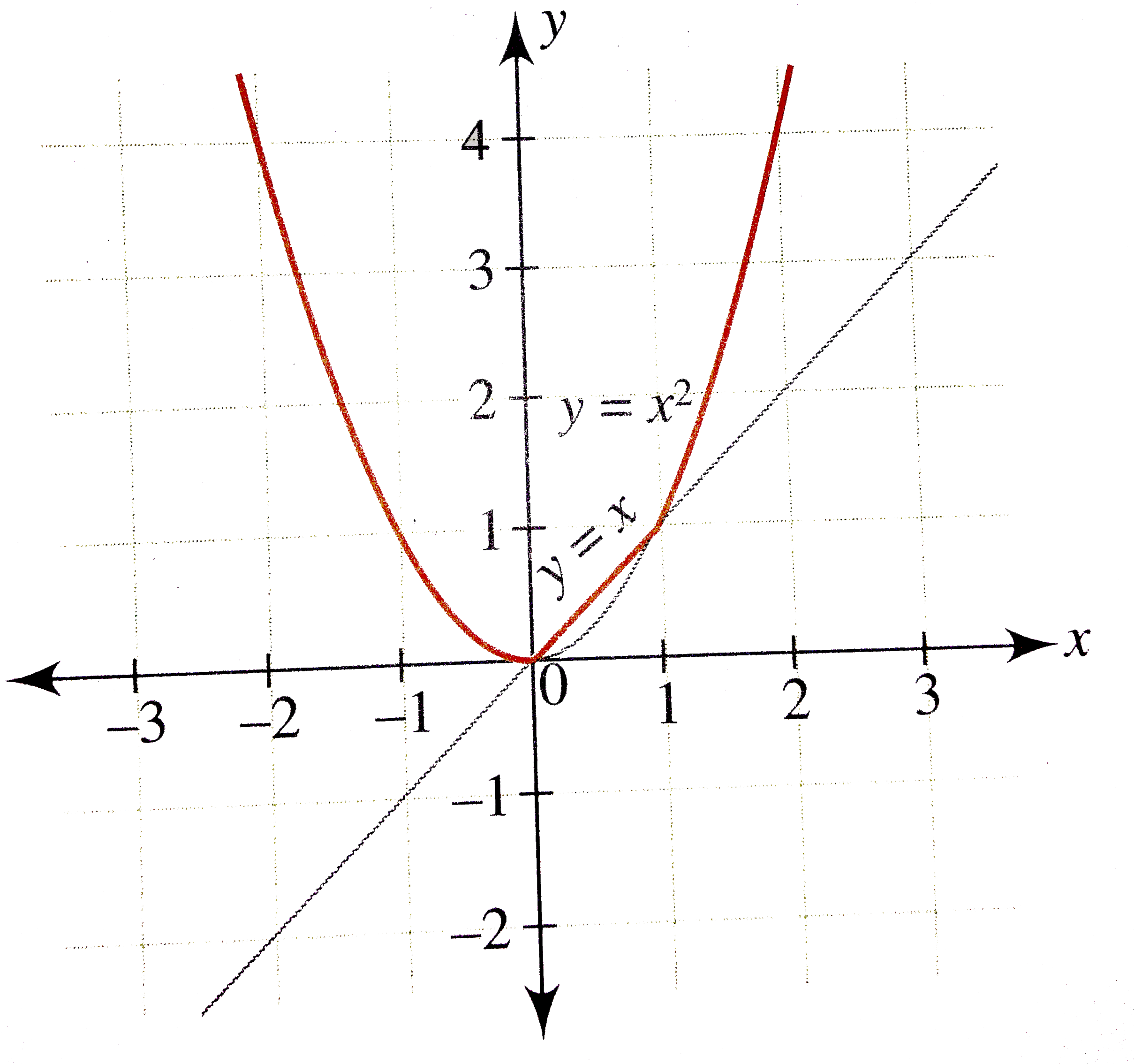



Draw The Graph Of The Function F X Max X X 2 And Write
Dec 24, 16 · Explanation First, find the derivative f '(x) = 3x2 6x 1 A horizontal tangent will have a slope of 0 The derivative represents the instantaneous rate of change of a function Set the derivative to 0 and solve for x 0 = 3x2 6x 1 x = −6 ± √62 − 4 ⋅ 3 ⋅ 1 2 ⋅ 3 x = −6 ± √24 6Entiable at x6= 0 with f0(x) = 0, since in that case f(x h) f(x) = 0 for all su ciently small h The sign function is not di erentiable at 0 since lim h!0 sgnh sgn0 h = lim h!0 sgnh h and sgnh h = (1=h if h>0 1=h if hThe graph of the absolute value function f (x) = x is similar to the graph of f (x) = x except that the "negative" half of the graph is reflected over the x axis Here is the graph of f (x) = x The graph looks like a "V", with its vertex at (0, 0) Its slope is m = 1 on the right side of the vertex, and m = 1 on the left side of the
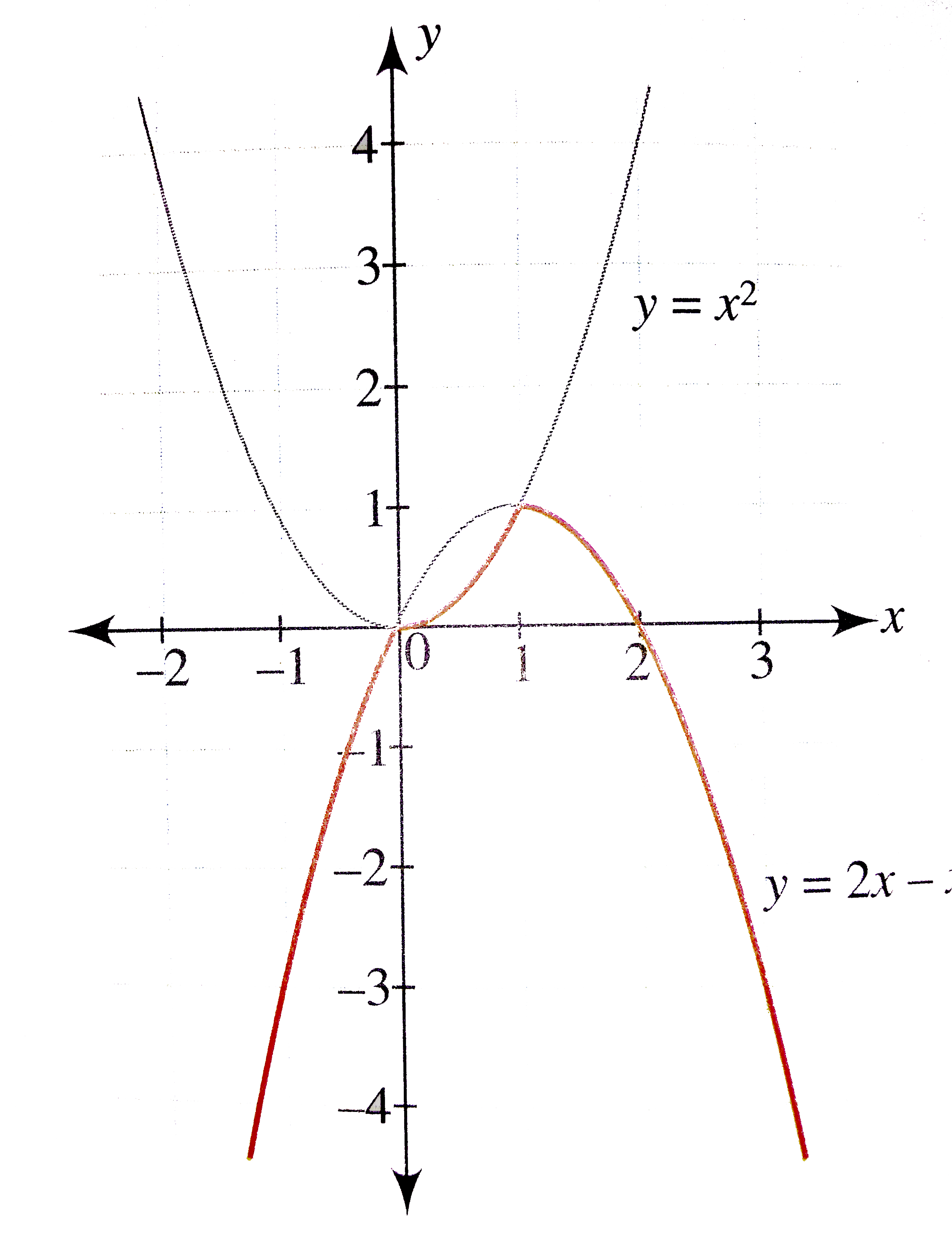



Draw The Graph Of The Function F X X X X 2 1 Le X Le 1




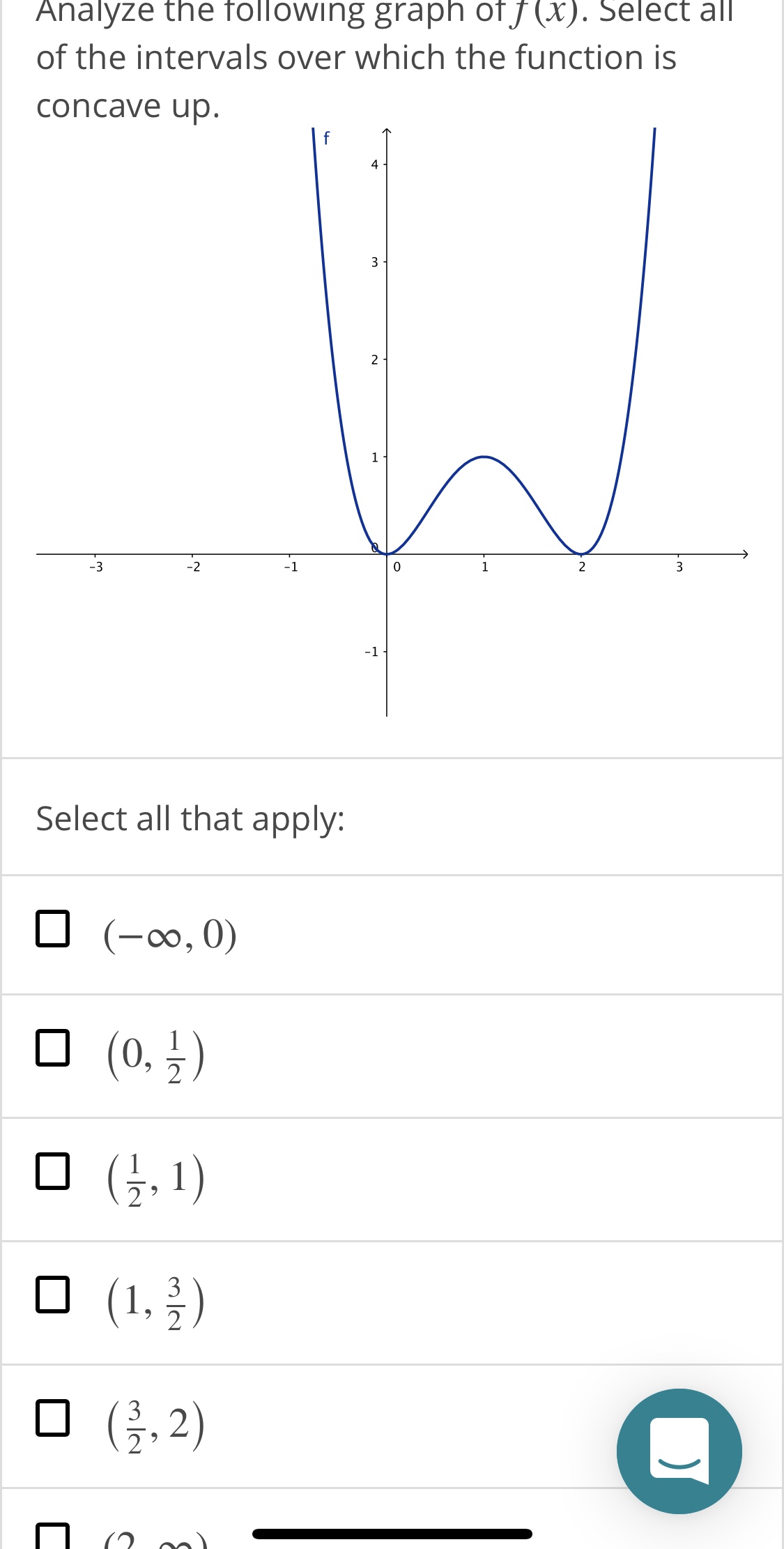
4 3 How Derivatives Affect The Shape Of A Graph Ppt Download
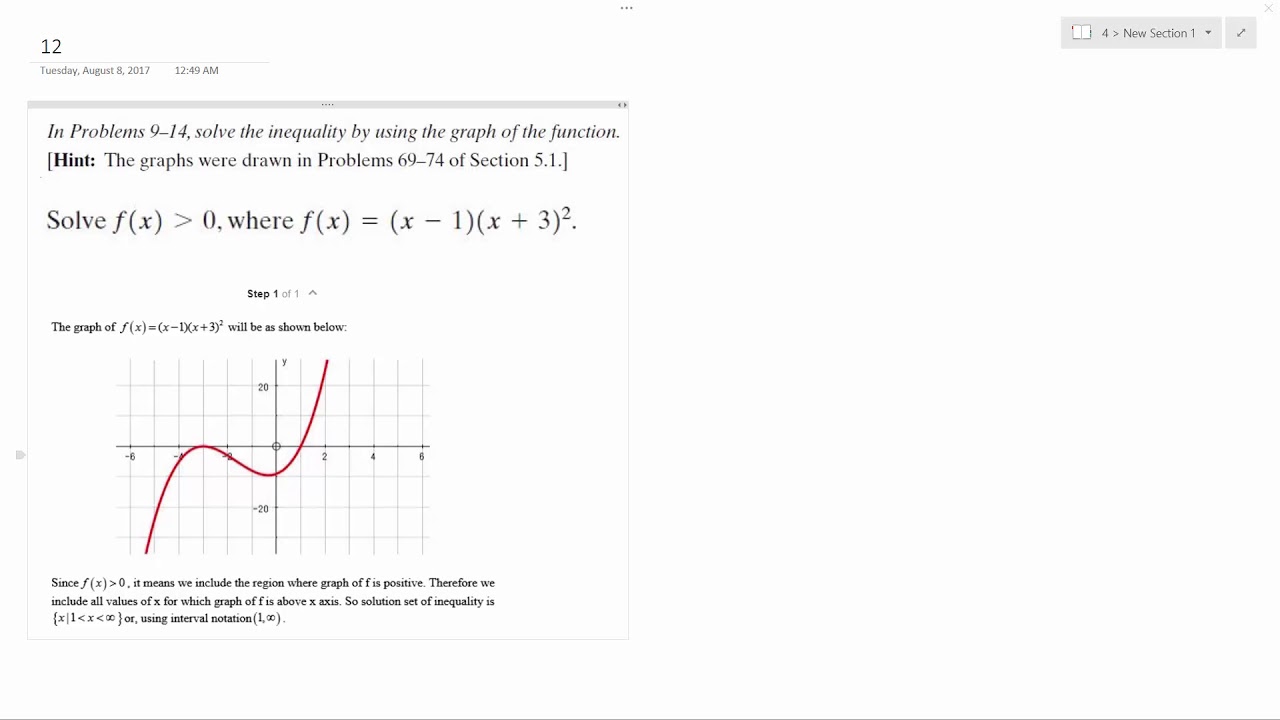
The graph of the continuous function ,f ′ shown in the figure above, has xintercepts at x =−2 and 3ln (5) 3 x = The graph of g on 4 0−≤ ≤x is a semicircle, and f ()05= (a) For 4 4,− Ap Calculus Ab Practice Exam Multiple Choice Problem 27 Youtube Calculus Limit Function Take The Limit As X Approaches C < 0 moves it downGRAPH OF f(x) = x^3 f(x) = x^3 graph how to draw graph of f(x)=x^3 y = x^3 graphNCERT CLASS 11 MATHS SOLUTIONS ex 23SUBSCRIBE TO MY CHANNEL TO GET MORE UPDAFree PreAlgebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators stepbystep Solved Sketch The Graph Of A Function That Satisfies All Chegg Com Step 4 Sketch The Graph Of F 5 4 14 F X X 4 X Manualzz Since f(−x) = e− (− x) 2 2 = e− 2 = f(x) and lim x→±∞ e− (−x)2 2 = 0, the graph is symmetry wrt the yaxis, and the xaxis is a horizontal asymptote • Wehave f0(x) = e−x 2 2 (−x) = −xe− x2 2 • Thus f ↑ on (−∞,0) and ↓ on (0,∞) • Atx = 0, f 0(x) = 0 Thus f(0) = e = 1 is the (only) local andIf f''(x) >0 on an interval, then f is concave upward on that interval d) If f''(x)(3) If f′(x) < 0 for all x in Io, then f is decreasing on I If we apply this theorem to f′ and f′′ instead of f and f′, we obtain results about concavity Corollary 2 Suppose f′ is continuous on the interval I and differentiable on its interior Io (1) If f′′(x) > 0 for all x in Io, then f is concave up on I Solved Sketch The Graph Of A Function That Satisfies All Chegg Com Ex Determine The Sign Of F X F X And F X Given A Point On A Graph Youtube Dec 21, · 33 1 A graph of a function f used to illustrate the concepts of increasing and decreasing Even though we have not defined these terms mathematically, one likely answered that f is increasing when x > 1 and decreasing whenJun 17, 18 · f (x) = 05 (4^x) f (2) = 05 * 4^2 f (2) = 05 * 16 = 8 The graph must contain point (2, 8) Now find f (3) f (x) = 05 (4^x) f (3) = 05 * 4^3 f (3) = 05 * 64 = 32 The graph must contain point (3, 32)Apr 13, 21 · Transcript Ex 51, 8 Find all points of discontinuity of f, where f is defined by 𝑓(𝑥)={ (𝑥/𝑥, 𝑖𝑓 𝑥≠0@&0 , 𝑖𝑓 𝑥=0)┤ Since we need to find continuity at of the function We check continuity for different values of x When x = 0 When x > 0 When x < 0 Case 1 When x = 0 f(x) is continuous at 𝑥 =0 if LHL = RHL = 𝑓(0) Since there are two different Ppt When F X 0 Or F X Is Undefined Powerpoint Presentation Id Drawing F X From F X Geogebra F is a function that is differentiable for all reals The value of f ′(x) is given for several values of x in the table below The table x 8,3,0,3,8 f'(x)4,2,0,4,5 If f ′(x) is always increasing, which statement about Calculus 1Lim x→−∞ f(x) = 1;Math g/math(x) = math/math(11/3) 3(x (2/3))^2 Therefore g(max) = (11/3) and it Why Isn T F X X Cos Frac Pi X Differentiable At X 0 And How Do We Foresee It Mathematics Stack Exchange Answered Analyze The Following Graph Of F X Bartleby Mathematical Consequences With the aid of the Mean Value Theorem we can now answer the questions we posed at the beginning of the section Consequence 1 If f0(x) = 0 at each point in an open interval (a;b), we can conclude that f(x) = C for some constant C for all x in the interval (a;b)The absolute value is the distance between a number and zero The distance between − 2 2 and 0 0 is 2 2 The final answer is 2 2 Substitute the x x value − 1 1 into f ( x) = x f ( x) = x In this case, the point is ( − 1, 1) ( 1, 1)Graph f (x)=0 f (x) = 0 f ( x) = 0 Rewrite the function as an equation y = 0 y = 0 Use the slopeintercept form to find the slope and yintercept Tap for more steps The slopeintercept form is y = m x b y = m x b, where m m is the slope and b b is the yintercept y = m x b y = m x b Find the values of m m and b b using the Graphing The Basic Functions Ap Calculus Ab Multiple Choice 1998 Exam Part B Videos Questions Solutions Step 3 Evaluate f at all endpoints and critical points and take the smallest (minimum) and largest (maximum) values Example 4 Find the absolute maximum and minimum of function f defined by f(x) = − x2 2x − 2 on − 2, 3 Solution to Example 4 Step 1 Find the first derivative of f f ′ (xA function may be thought of as a rule which takes each member x of a set and assigns, or maps it to the same value y known at its image x → Function → y A letter such as f, g or h is often used to stand for a functionThe Function which squares a number and adds on a 3, can be written as f(x) = x 2 5The same notion may also be used to show how a function affects particular values Answer In Calculus For Desmond Answered Sketch The Graph Of A Function That Bartleby The Graph Of Y F X Is Shown Below What Are All Of The Real Solutions Of F X 0 Brainly Com Sketch A Possible Graph Of A Function F That Chegg Com The Graph Of Y F X Is Shown Below What Are All Of The Real Solutions Of F X 0 Brainly Com Finding Values Of Derivative Given F Graph Mathematics Stack Exchange Answered Sketch The Graph Of A Function That Bartleby Section 3 4 Concavity And The Second Derivative Test Ppt Download How Do You Sketch The Graph That Satisfies F X 0 When X 3 F X 0 When X 3 And F 3 5 Socratic Match The Conditions F X 0 And F 0 On A B With Chegg Com Sketch The Graph Of A Function That Satisfies All Of Chegg Com 1 2 Sec4 3 How Derivatives Affect The Shape Of A Graph Ppt Download F X 0 And F X 0 Graph L Hopital S Rule Wikipedia 5 1 Derivatives And Graphs Pdf Free Download Solved 1 The Graph Of F X Is Continuous And Decreasing With An X Intercept At X 0 Which Of The Following Statements Is True Course Hero Graphing The Basic Functions Solved Sketch The Graph Of A Function That Satisfies All Chegg Com Draw The Graph Of Each Of The Following Constant Functions I F Quadratic Example For What Values Of X Is F X Greater Than 0 Youtube Answered Sketch The Graph Of A Differentiable Bartleby The Shape Of A Graph Docsity The Mean Value Theorem And Curve Sketching Ppt Video Online Download 1 Polnts Scalce18 4 3 029 Sketch The Graph Of A Chegg Com If F X 1 3 F X 1 5 F X 2 F X 0 For All X Element Of R And Lim Askiitians Find Lim Limits N To Infty Int 0 1 F N X Dx With F 0 X X And F N 1 X Sin Pi F N X Mathematics Stack Exchange Limits Of Combined Functions Video Khan Academy Solve F X Greater Than 0 Where F X X 1 X 3 2 Youtube Sketch The Graph Of A Function That Satisfies All Of Chegg Com 10 Sketch A Graph Of One Function F X With All Of Chegg Com 4 3 How Derivatives Affect The Shape Of A Graph Ppt Download Solved Sketch The Graph Of A Function That Satisfies All Chegg Com




















































































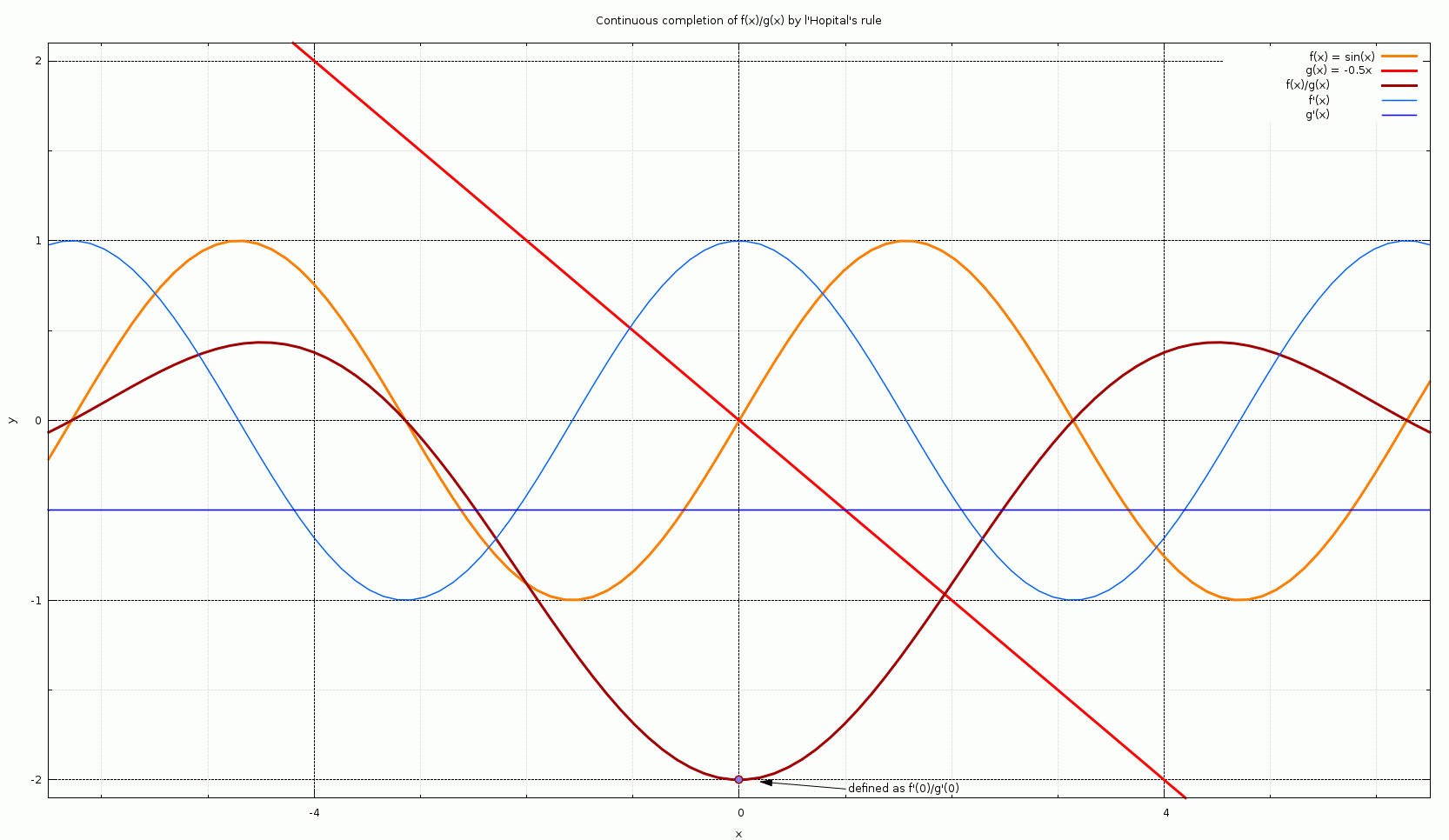










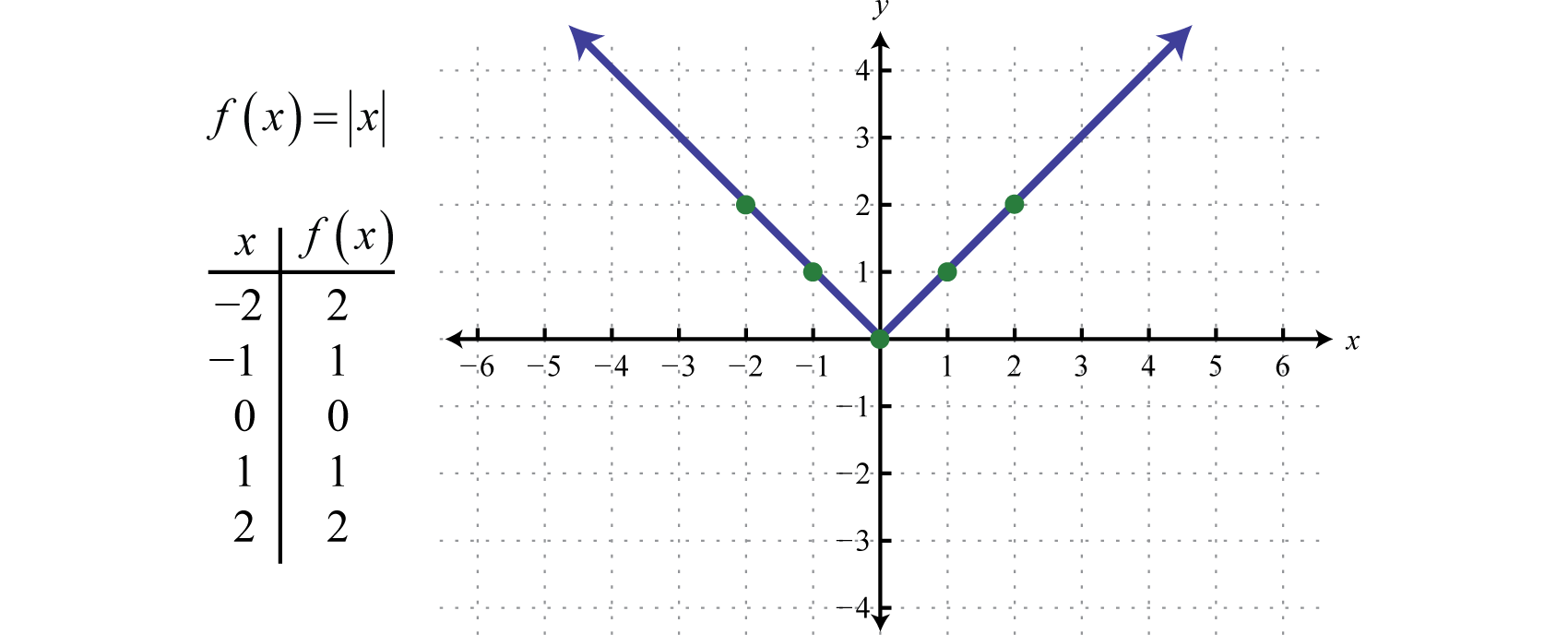



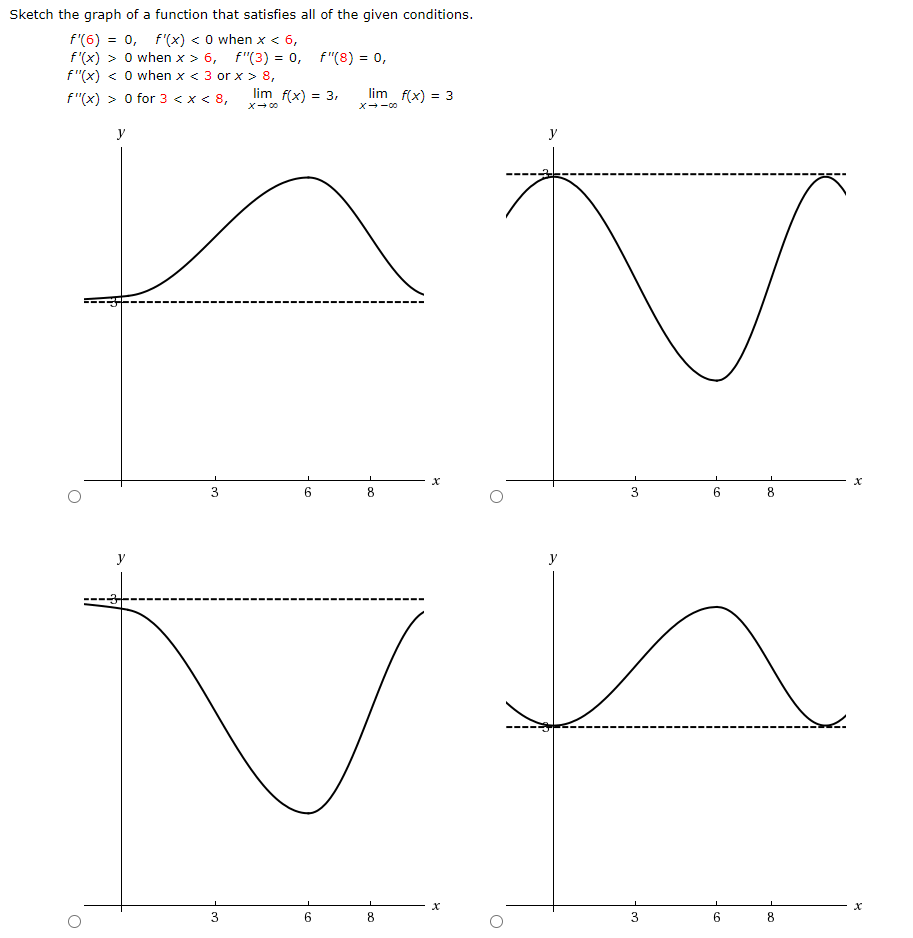










































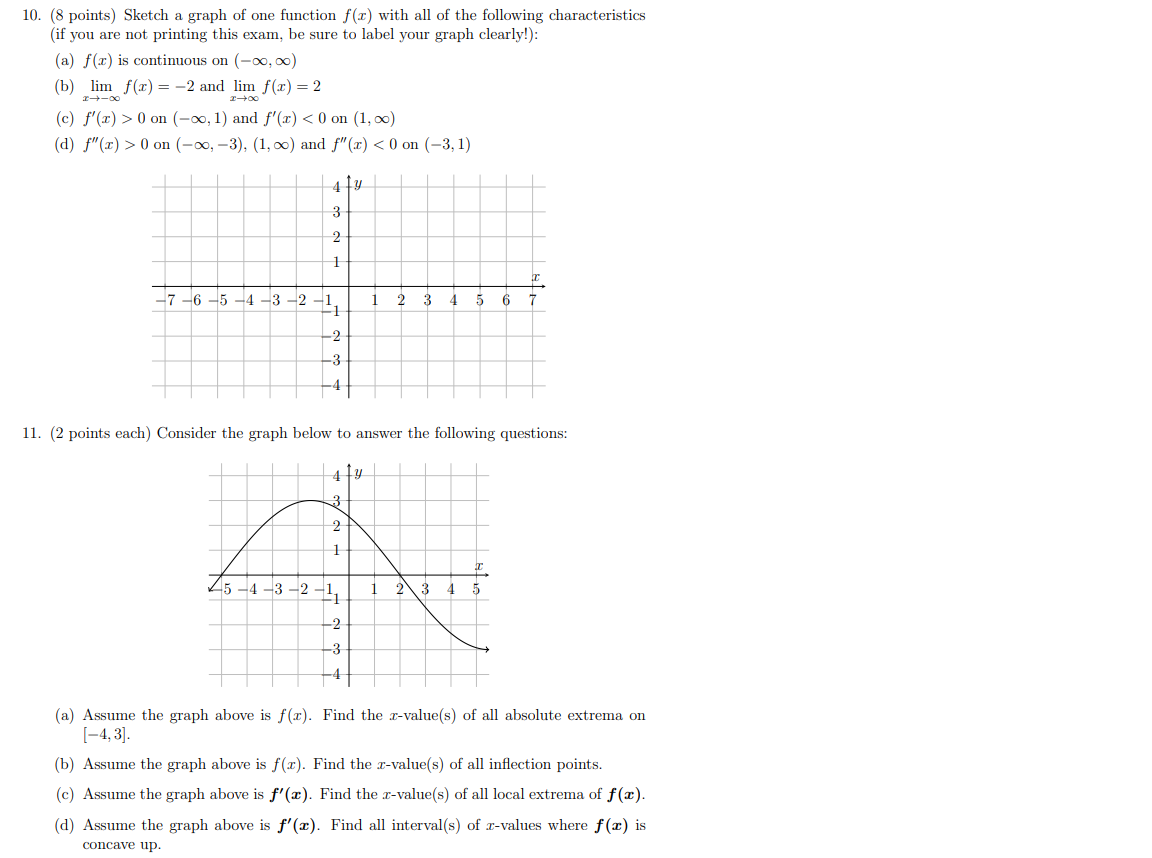



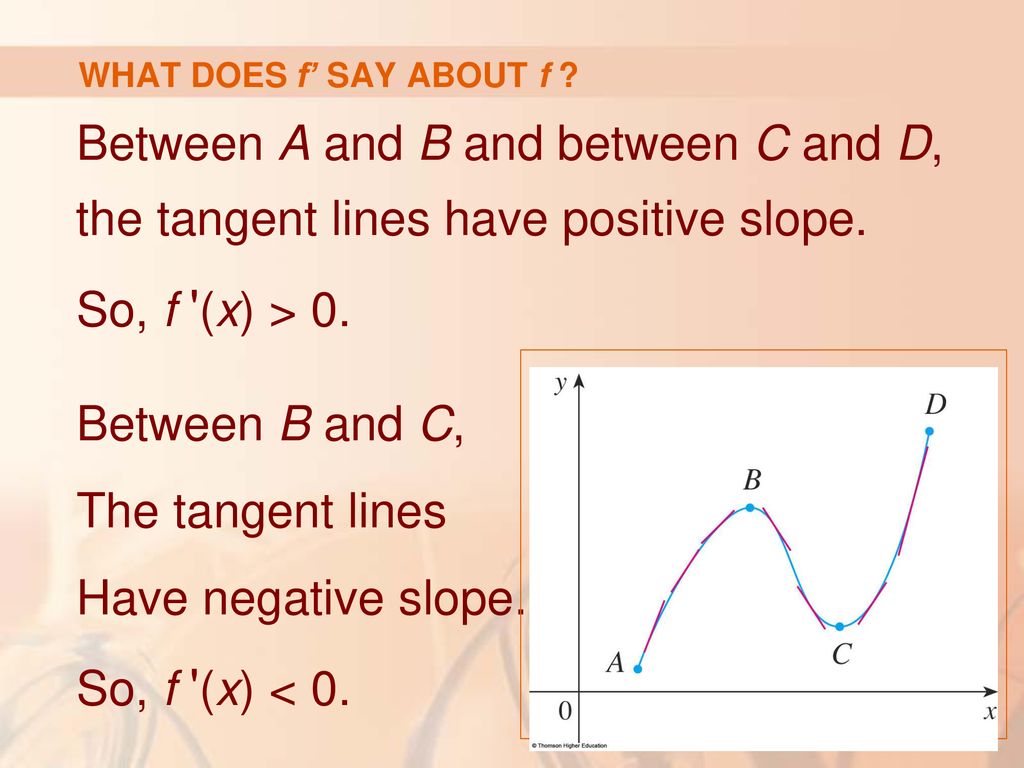



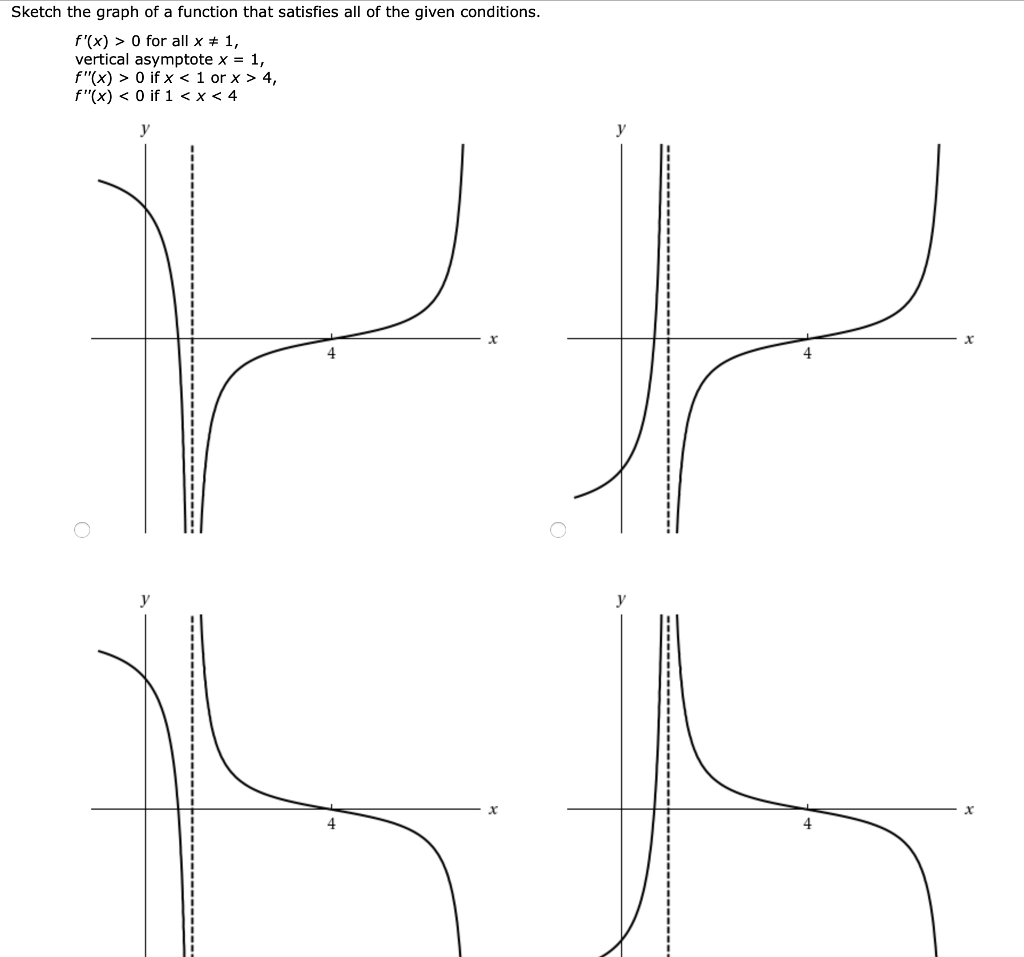






0 件のコメント:
コメントを投稿